1213 今日总结

今日工作

使用 matrix 的坑：

原本我使用正则的方式去获取 transform 的 translateX, translateY, rotate, scale 参数

const img = document.querySelector('#img')
const styleStr = img.style.transform;

const patt = /正则匹配/
const value = styleStr.match(patt)

但是这种方式获取，translateX, translateY, scale 都是很好用的，唯一 rotate 的获取很麻烦，远远不如 rotate(30deg) 这种方式直白

看操作：

const transformAttr = document.getComputedStyle(dom).transform; // 返回 matrix 数组
// matrix( a,       b,    c,        d,      e,            f    ) 
// matrix(scale, skew, rotate角度, scale, translateX, translateY)


// 这里的 rotate 不能直接获取，需要进行  sin, cos 进行计算才能得到；
// matrix(cosθ, sinθ, -sinθ, cosθ, 0, 0)
// x' = xcosθ- ysinθ + 0 = xcosθ-ysinθ
// y' = xsinθ + ycosθ + 0 = xsinθ+ycosθ

总而言之：

如果是为了获取 rotate 属性，还不如直接使用正则的方式方便快捷，但是，需要注意的是 dom.style.transform 的属性只能在 style 设置，类里面的，此方法无法获取到；

读读张鑫旭老师的文章学习学习

手撕代码

防抖节流等各种手写，http和网络，浏览器原理，性能优化，Webpack

选择排序-菜鸟教程-算法系列结合动图和例子学习

选择排序

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。

再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

重复第二步，直到所有元素均排序完毕。

算法复杂度：O(n²)


function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                minIndex = j;                 // 将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}


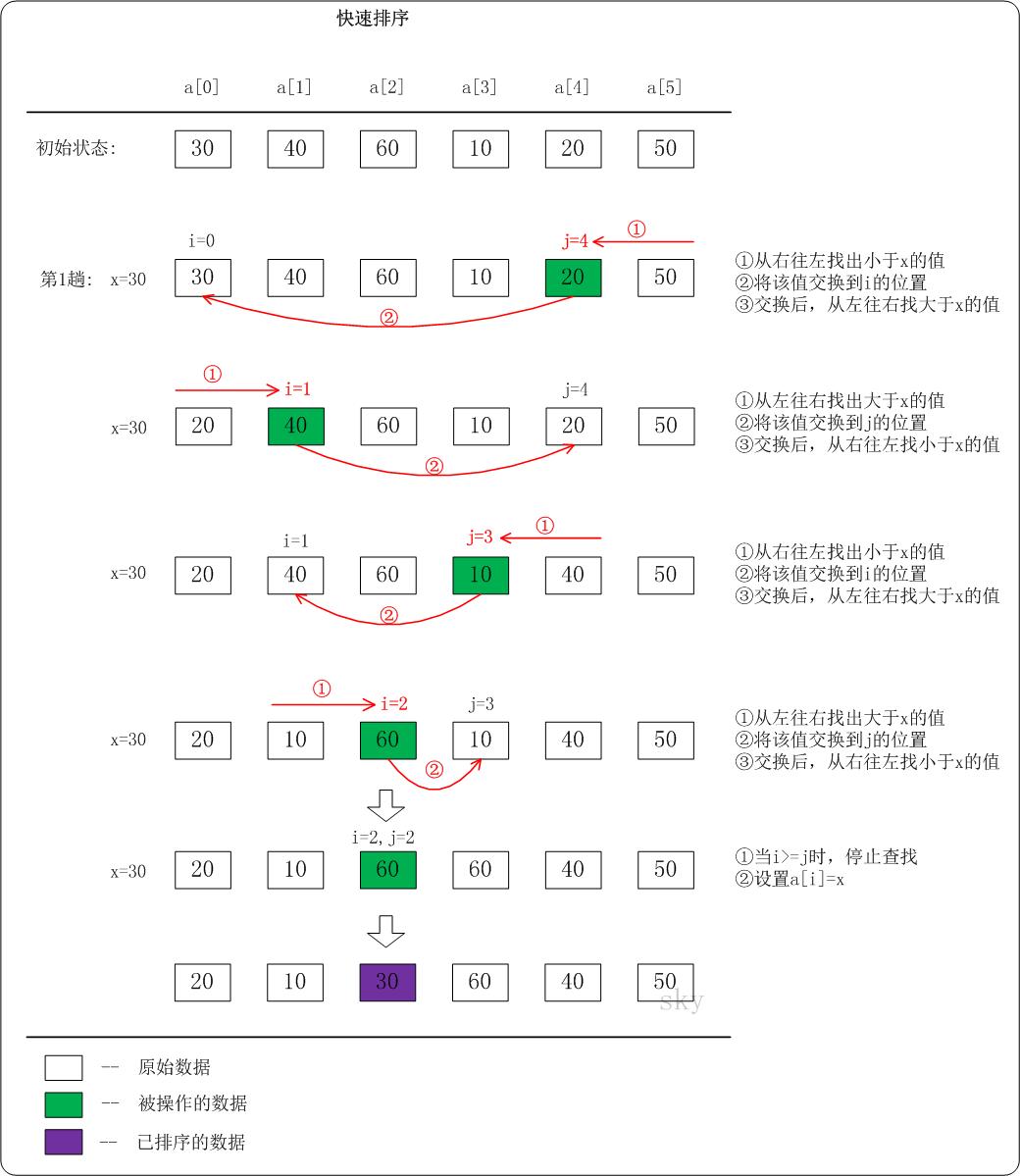
selectionSort([5,4,3,2,1,8]) // [1, 2, 3, 4, 5, 8]

快速排序：

参考：快速排序


function quickSort(arr, l = 0, r = arr.length -1) {
    if (l < r) {
        let i, j, x;
        i = l,
        j = r,
        x = arr[i];
        while (i < j) {
            while (i < j && arr[j] > x) {
                j-- // 从右向左找第一个小于x的数
            }
            if (i < j) {
                arr[i ++] = arr[j]
            }
            while (i < j && arr[i] < x) {
                i++ // 从左向右找第一个大于x的数
            }
            if (i < j) {
                arr[j--] = arr[i]
            }
        }
        arr[i] = x;
        quickSort(arr, l, i-1) // 递归
        quickSort(arr, i+1, r) // 递归
    }
    return arr
}

quickSort([5,4,3,2,1,8])

1213 今日总结 ​

今日工作 ​

手撕代码 ​

1213 今日总结

今日工作

手撕代码