二分查找法
- 算法思想:
- 常用策略/模板:
- 时间复杂度:log2 N
- 练习题
例题:
- 704 二分查找
- 35 搜索插入位置
- 162 寻找峰值
- 74 搜索二维矩阵
找位置/目标值
难度简单
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
- 方法:
- 题解:
- 答案:
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function(nums, target) {
if (!nums.length) return -1
let left = 0, right = nums.length - 1;
while(left <= right) {
// left + (right - left)/2 的作用是避免 left + right 超过边界
let mid = Math.floor(left + (right - left) / 2)
if (nums[mid] === target) return mid
// 中间值小于目标值,左指针右移
if (nums[mid] < target ) {
left = mid + 1
} else {
// 中间值大于目标值,右指针左移
right = mid - 1
}
}
return -1
};
难度简单
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
- 方法:
- 题解:
- 答案:
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var searchInsert = function(nums, target) {
if (!nums || !nums.length) return 0
let l = 0, r = nums.length - 1;
// 先用 二分法做
while(l <= r) {
let mid = Math.floor(l + (r-l)/2)
if (nums[mid] === target) return mid
if (nums[mid] < target) {
l = mid + 1
} else {
r = mid -1
}
}
// 二分法没找到,说明不存在,那么此时 左指针和右指针中间,就是 target 该插入的位置,因为 l = mid + 1,所以直接取 l
return l
};
难度中等
峰值元素是指其值大于左右相邻值的元素。
给你一个输入数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
**进阶:**你可以实现时间复杂度为 O(logN) 的解决方案吗?
- 方法:
- 题解:
- 答案:
/**
* @param {number[]} nums
* @return {number}
*/
var findPeakElement = function(nums) {
if (!nums || !nums.length) return -1
nums[-1] = -Infinity
nums[nums.length] = -Infinity
let l = 0, r = nums.length -1
while (l < r) {
let mid = Math.floor(l + (r-l)/2)
// 如果中间值小于右边值,则右边可能为峰值,左指针右移
if (nums[mid] < nums[mid + 1]) {
l = mid + 1
} else {
// 如果中间值大于右边值,则左边可能为峰值,右指针左移
r = mid
}
}
return l
};
难度中等
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
- 每行中的整数从左到右按升序排列。
- 每行的第一个整数大于前一行的最后一个整数。
示例 1:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
示例 2:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
方法:
- 方法1:直接将二维转换成 一维数组,再利用二分法;
- 方法2:在二维数组中利用二分法做
- 难点:利用二分法做,左右指针的移动,以及中间值的位置,看图:
二维矩阵中,某一个元素的坐标转换成一维的公式:为
(x,y) === x * 列数量 + y,如:(1,2) === 1 * 4 + 2为 第 6 个元素;反过来,我们从一维角度推出二维坐标则是:
ele = matrix[Math.floor(mid / col)][mid % col],横坐标用 商数,纵坐标用余数。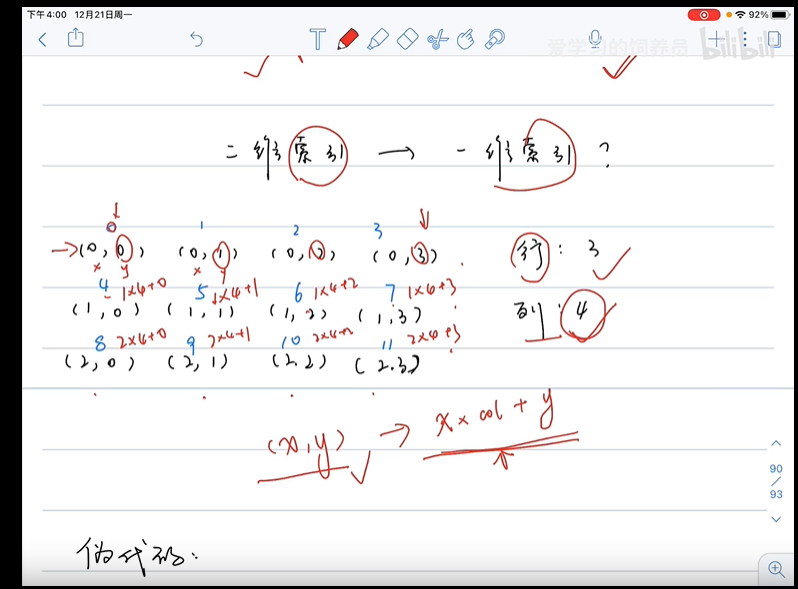
题解:
答案:
方法1:
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function(matrix, target) {
const arr = matrix.reduce((pre, cur) => {
const result = pre.concat(cur)
return result
}, [])
return arr.includes(target)
};
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function(matrix, target) {
return matrix.flat().indexOf(target) > -1;
};
方法2:
var searchMatrix = function(matrix, target) {
if (!matrix || !matrix.length) return false
// 行数
const row = matrix.length
// 列数
const col = matrix[0].length
// 左指针为 0 ,右指针 为 二维数组的最后一个子数组最后一个位置
let l = 0, r = row * col;
// 指针按照一维数组来移动,即左右移动;中间值则用 2 个坐标值来计算
while(l < r) {
// 有序二维数组中,取中间值的位置 (r-l) / 2
let mid = Math.floor(l + (r - l)/2)
// 核心代码在这里
// 若二维数组为 5*4, mid 为 10,则位置为第 3 行第2个;
// 对应坐标计算为:横坐标 = mid % 列 ; 纵坐标 = mid / 行数
const ele = matrix[Math.floor(mid / col)][mid % col]
if (ele === target) {
return true
} else if (ele > target) {
// 右指针左移
r = mid
} else {
l = mid + 1
}
}
return false
};