BackTracking 回溯法
- 类似枚举
- 本质上还是递归
关键词:关键路径,最优解。
例题:
- 22 括号生成
- 78 代表性回溯题
- 77 组合
- 46 全排列
- 经典:八皇后,数独
题型一
难度中等1640收藏分享切换为英文接收动态反馈
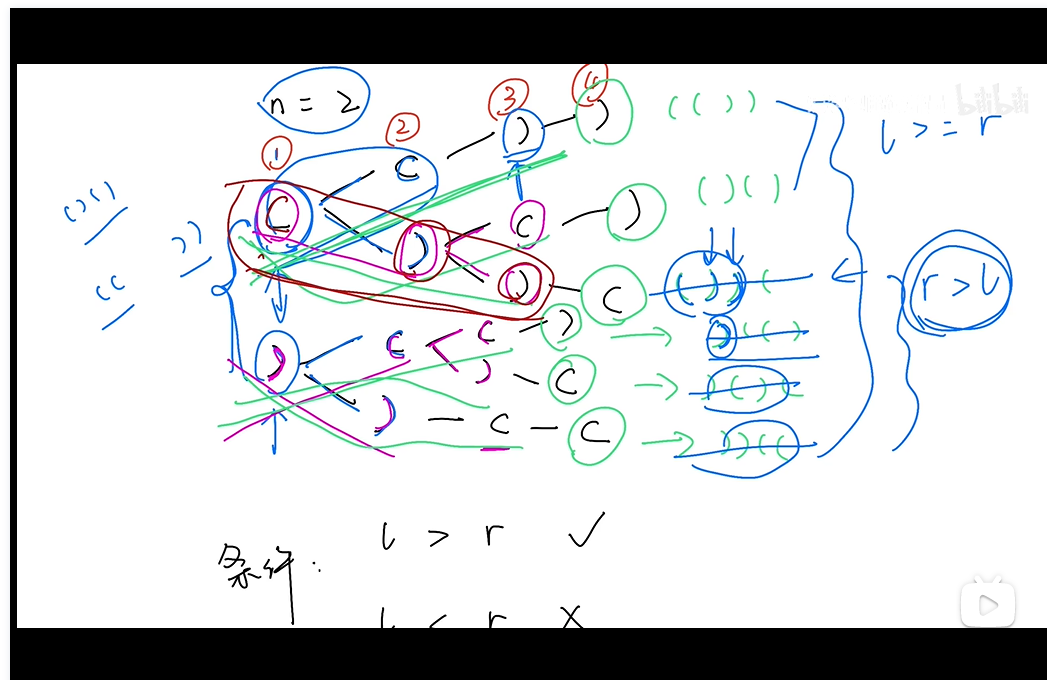
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
提示:
1 <= n <= 8
- 方法:
- 题解:https://mp.weixin.qq.com/s/VslFExUGNkYUNWXd91zbkQ
- 视频:https://www.bilibili.com/video/BV1sy4y1q79M?p=65&spm_id_from=pageDriver
- 说明:
- 代码
/**
* @param {number} n
* @return {string[]}
*/
var generateParenthesis = function(n) {
const list = []
backtracking(n, list, 0, 0, "");
return list;
};
function backtracking(n, result, left, right, str) {
// 右边括号数量大于左边,表示无效括号组合
if (right > left) {
return;
}
// 左右两边括号数量相等
if (left == n && right == n) {
result.push(str);
return;
}
// 左边少了,则左边 + 1
if (left < n) {
backtracking(n, result, left+1, right, str+"(");
}
// 右边少了,则右边 + 1
if (right < left) {
backtracking(n, result, left, right+1, str+")");
}
}
难度中等1059收藏分享切换为英文接收动态反馈
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
解法:
- 方法:
- 视频:https://www.bilibili.com/video/BV1sy4y1q79M?p=66
- 解法:https://mp.weixin.qq.com/s/QyflseNcsZCYG1XnorGx3Q
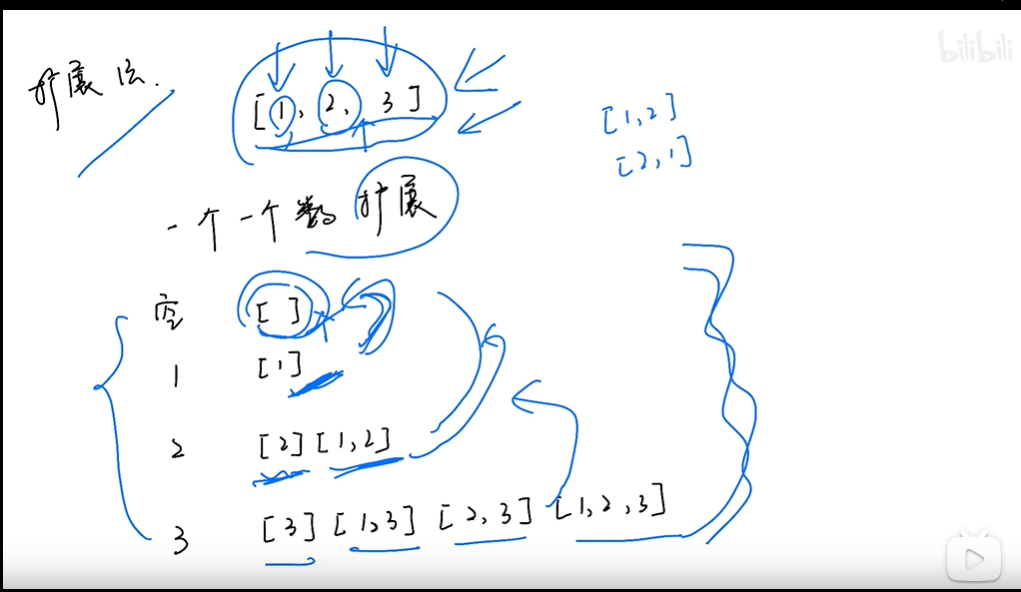
- 拓展法
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function(nums) {
// 例如 nums = [1,2,3]
const result = []
result.push([])
// 遍历所有 nums
for (let i = 0; i < nums.length; i ++) {
// 定义临时 子数组-> 子集 数组
const sub = []
// 例如 result = [[], [1], [1,2]]
for (let m = 0; m < result.length; m++) {
// 定义临时变量,暂存 result 的 某一个 子集,也是我们要的结果
// 例如 result[m] = [1,2], 拷贝一份 temp => [1,2]
const temp = [].concat(result[m])
// 单数子集,比如 1, 或者 2, 或者 3
temp.push(nums[i])
// 多数子集,比如 [[1], [1,2], [1,2,3]]
sub.push(temp)
}
// 一个个遍历子集,把他们放入 result 中
for (let k in sub) {
result.push(sub[k])
}
}
return result
};
- 递归回溯法
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function(nums) {
const result = []
for (let i=0; i<= nums.length; i++) {
backtracking(nums, result, i, 0, []);
}
return result
};
// 参数说明 result 子集容器,要找的子集的长度 length,要从哪个位置开始找 index; sub 用于缓存子集结果
function backtracking(nums, result, length, index, sub) {
// 退出条件-子集的长度等于要找的 index
if (sub.length === length) {
result.push([].concat(sub))
return
}
for (let i = index; i< nums.length; i++) {
sub.push(nums[i])
backtracking(nums, result, length, i+1, sub);
// 删掉最后一个 子集,避免在下一次回溯的时候重复
sub.pop()
}
}
- DFS 法
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function(nums) {
const result = []
dfs(nums, result, 0, [])
return result
};
function dfs (nums, result, index, sub) {
result.push([].concat(sub))
if (nums.length === index) return
for (let i = index; i < nums.length; i++) {
sub.push(nums[i]);
dfs(nums, result, i+1, sub);
sub.pop()
}
}